Introduction

这是一份用Typst写成的笔记

Chapter 1: 市场

我们将主要使用 Varian, H. R. (2014) Intermediate Microeconomics: A Modern Approach. 9th ed. New York: W.W. Norton& Company.

经济学的研究 → 建立模型. e.g. 美国中西部一个中等大小的大学城的住房市场. 邻近大学的住房在内城区, 其余的在外城区, 外城区的住房供应量很大, 价格固定在某个水平上, 我们只考察内城区住房价格的决定因素和谁将住在内城区. 我们说外城区的住房价格是外生变量, 内城区的住房价格是内生变量.

最优化与均衡

• 最优化原理: 人们总是选择他们能支付得起的最佳消费方式.
• 均衡原理: 价格会自行调整, 直到人们的需求数量与供给数量相等.
• 保留价格: 某人愿意支付的最高价格.
• 需求曲线: 一条把需求和价格联系起来的曲线.

如果一个人持有保留价格 $p$, 意味着他支付价格 $p$ 和住在外城区都是可以的, 因此按照价格 $p^{\ast }$ 出租的住房数量正好是所持保留价格大于或等于 $p^{\ast }$ 的人数, 画成下图 Figure 1.1:

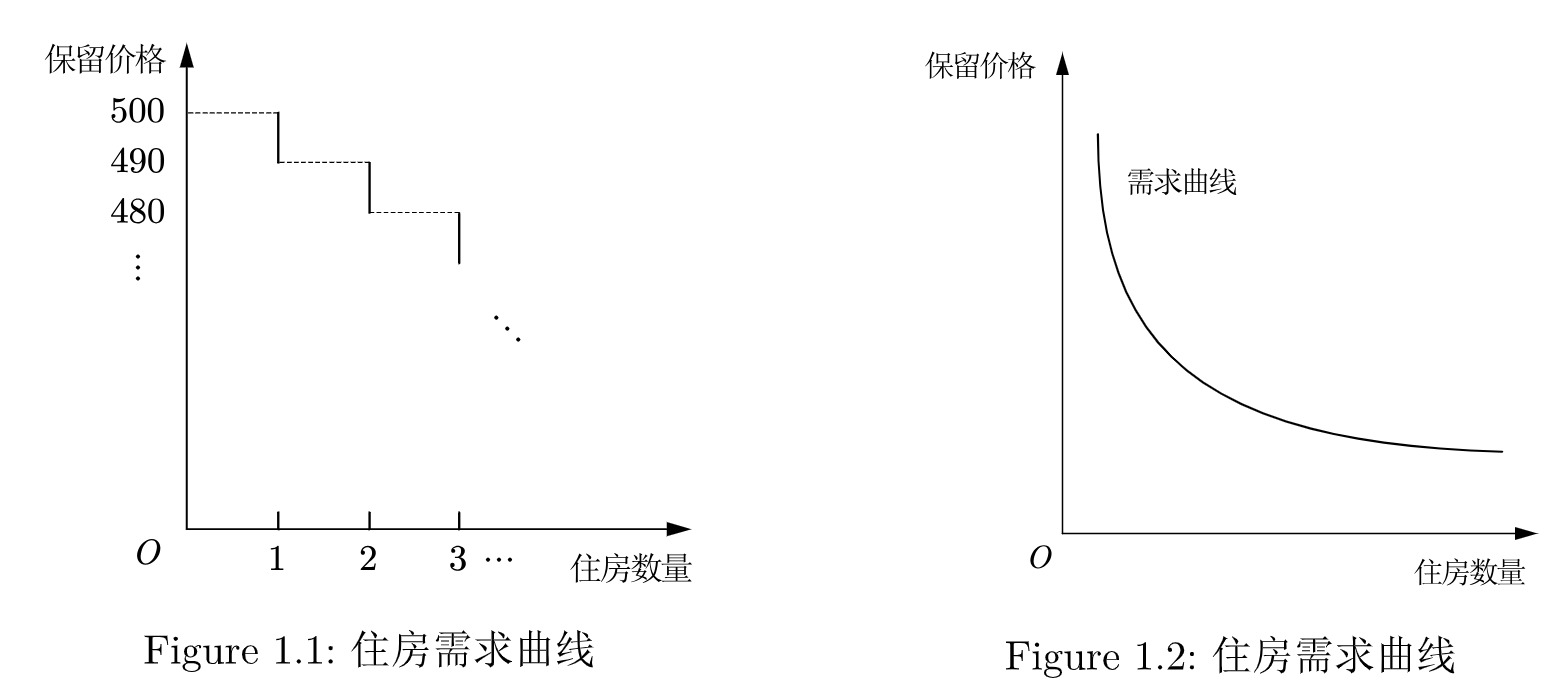
由于存在大批需求者, 价格间的跳跃很小, 需求曲线的倾斜通常是平缓的, 如 Figure 1.2.

供给曲线

在短期内, 住房的数量多少是固定不变的. 当然, 如果是考虑长期的情况, 住房的数量必然随着建设或者某种别的因素增加或者减少.

市场均衡

我们用 $p^{\ast }$ 表示住房需求量等于住房供给量时的价格. 这就是住房的均衡价格. 在这个价格水平上, 愿意至少支付 $p^{\ast }$ 的消费者可以找到房子, 而每个房东也可以按照这个价格出租房子, 双方都没有理由改变他们的行为. 这就是我们所说的均衡, 即人们的行为不会有任何的变化. 正如下图 Figure 1.3.

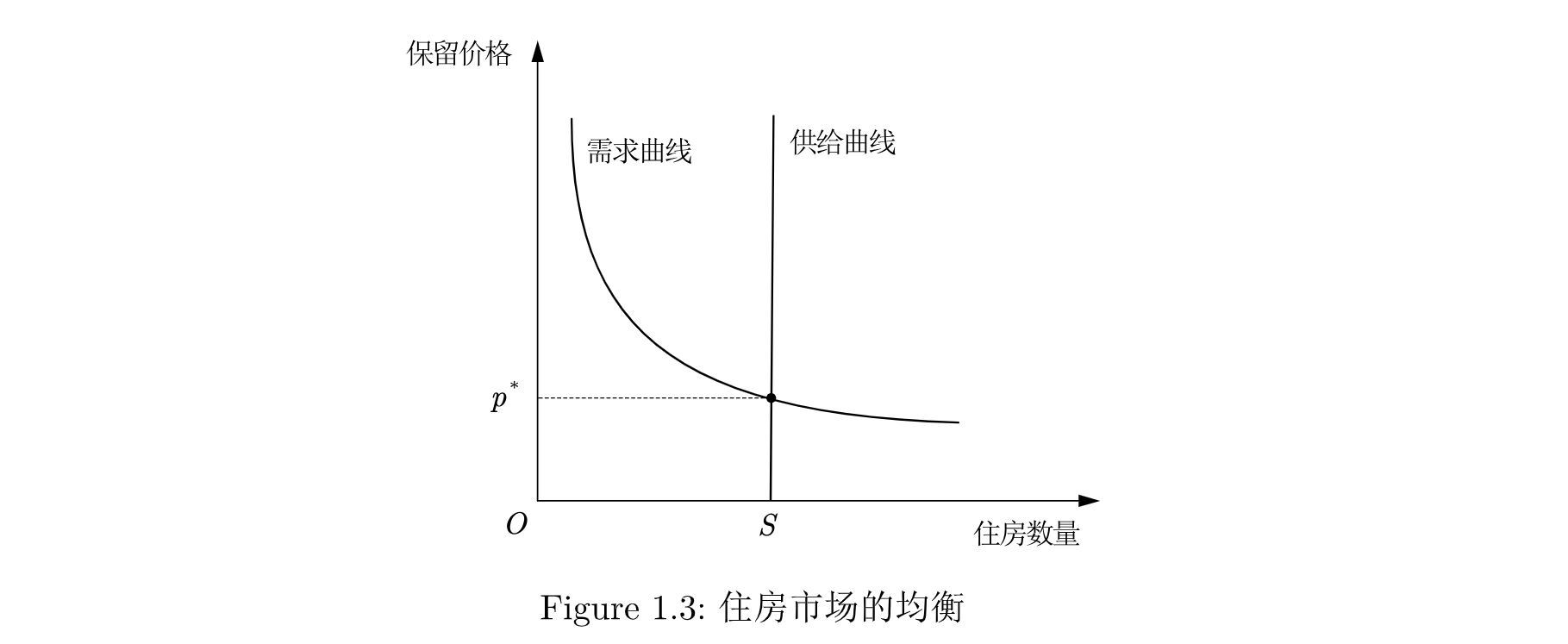
比较静态分析

比较静态分析: 当市场各个方面发生变化的时候, 分析均衡状态的变动. p.s. 只关心两个“静态”均衡之间的比较, 而不关心市场是如何从一个均衡到另一个均衡的.

现在我们先假设住房供给增加了:

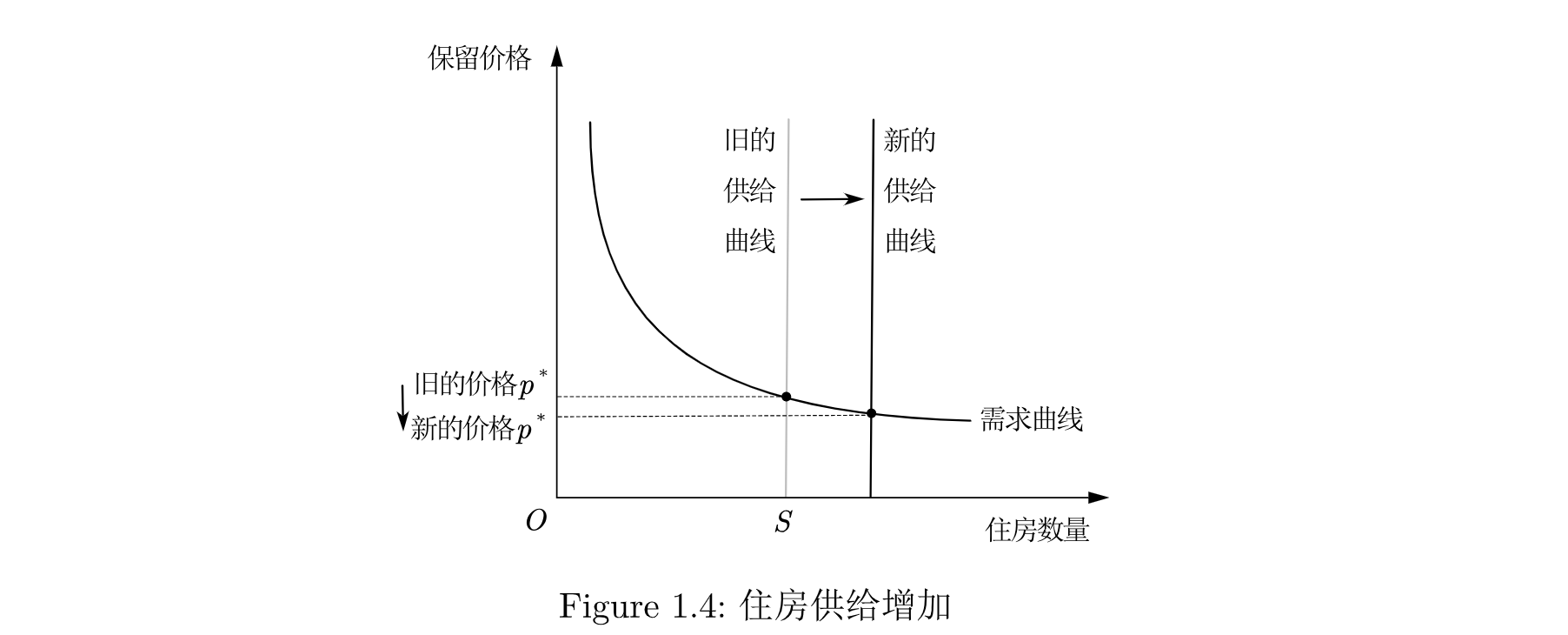
从Figure 1.4中我们就能清楚地看到均衡价格将会下降.

现在, 假设有一个房地产开发商决定把一些公寓改造成个人所有的公寓, 那么其余住房的价格会有怎样的变动呢?

假设私人公寓的购买者已经居住在内城区, 也就是那些愿意支付高于 $p^{\ast }$ 价格的人, 那么假设有10个人决定购买住房, 那么住房的需求曲线就会向左移动10个单位, 同时供给曲线也会向左移动10个单位, 结果最后均衡价格就会保持不变.

现在, 假设对住房征税, 每个房东必须为他的房子支付一定比例的税. 那么当前的住房供给不变, 均衡价格 $p^{\ast }$ 已经是房东所能索取的最高价格了, 房东无法抬高住房价格, 所以税收必须由房东来支付.

配置住房的其他方法

• 垄断: 市场被某一产品的单一卖主所支配的情况.
• 价格歧视垄断者: 只有一个占支配地位的房东, 他拥有所有的住房. 他可以按不同的价格出租房子. p.s. 他会按照保留价格从高到低出售给消费者, 使得最后一个人支付 $p^{\ast }$, 从 $0$ 到 $p^{\ast }$ 和需求曲线围起来的面积就是房东的收益.
• 一般垄断者: 他被迫按照同样的价格出租每一套房子. 设垄断者定价为 $p$, 此时的需求为 $D(p)$, 那么收益就是 $pD(p)$, 他应该在这个式子取最大值时定价.
• 房租管制: 制定了房租的最高值为 $p_{\text{max}}$.

帕累托效率

• 帕累托改进: 如果可以找到一种配置方法, 在其他人的境况没有变坏的情况下, 的确能够使得一些人的境况变得更好一点, 那么就存在帕累托改进.
• 帕累托低效率: 如果一种配置方法存在帕累托改进, 那么它就被称为帕累托低效率的.
• 帕累托有效率: 如果一种配置方法不存在任何的帕累托改进, 那么它就被称为帕累托有效率的.

配置住房的不同方法的比较

任何一个拥有内城区住房的人一定要比拥有一套外城区住房的人持有一个更高的保留价格. 否则, 他俩可以交易使得双方的境况都变好, 违反了帕累托有效率配置.

竞争市场, 价格歧视垄断者 → 帕累托有效率的.

一般垄断者, 房租管制 → 帕累托低效率的.

长期均衡

住房的供给不再固定不变.

Chapter 2: 预算约束

预算约束

• 消费束: $X\equiv (x_1,x_2)$ 表示消费者选择商品 $x_1$ 的消费量和 $x_2$ 的消费量. p.s. 两种商品的概括性很强, 因为我们可以把另外的一种商品看成是消费者想要消费的其他一切商品的总和, 代表了一种复合商品.
• 预算约束: 假设我们知道了两种商品的价格 $(p_1,p_2)$ 以及消费者要花的货币总数 $m$, 那么预算约束就可以被写为 $$p_1{x}_1+p_2{x}_2\le m.$$
• 预算集: 我们把当价格为 $(p_1,p_2)$ 和收入为 $m$ 时能够负担的消费束称为消费者的预算集.
• 预算线: 预算线指的是所需费用正好等于 $m$ 的一系列消费束, 即 $$p_1{x}_1+p_2{x}_2=m.$$

下面是预算约束的图示

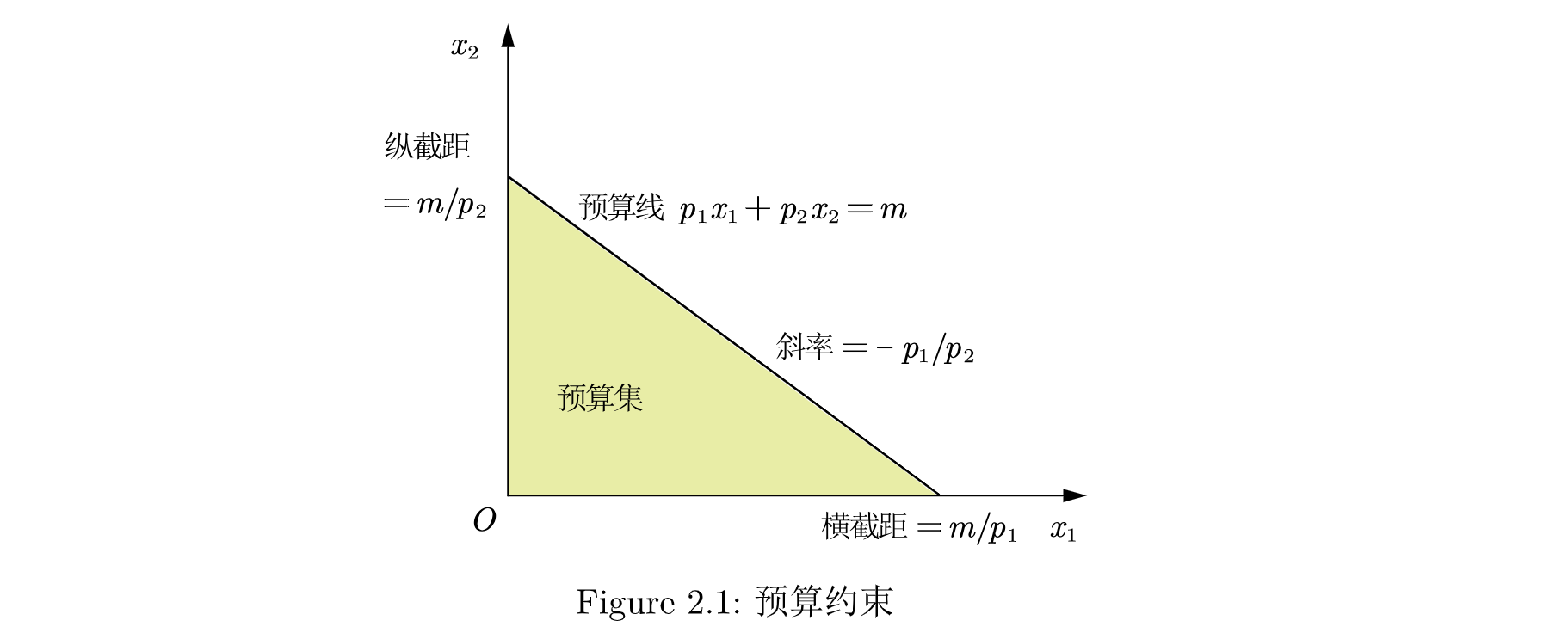
预算线的变动

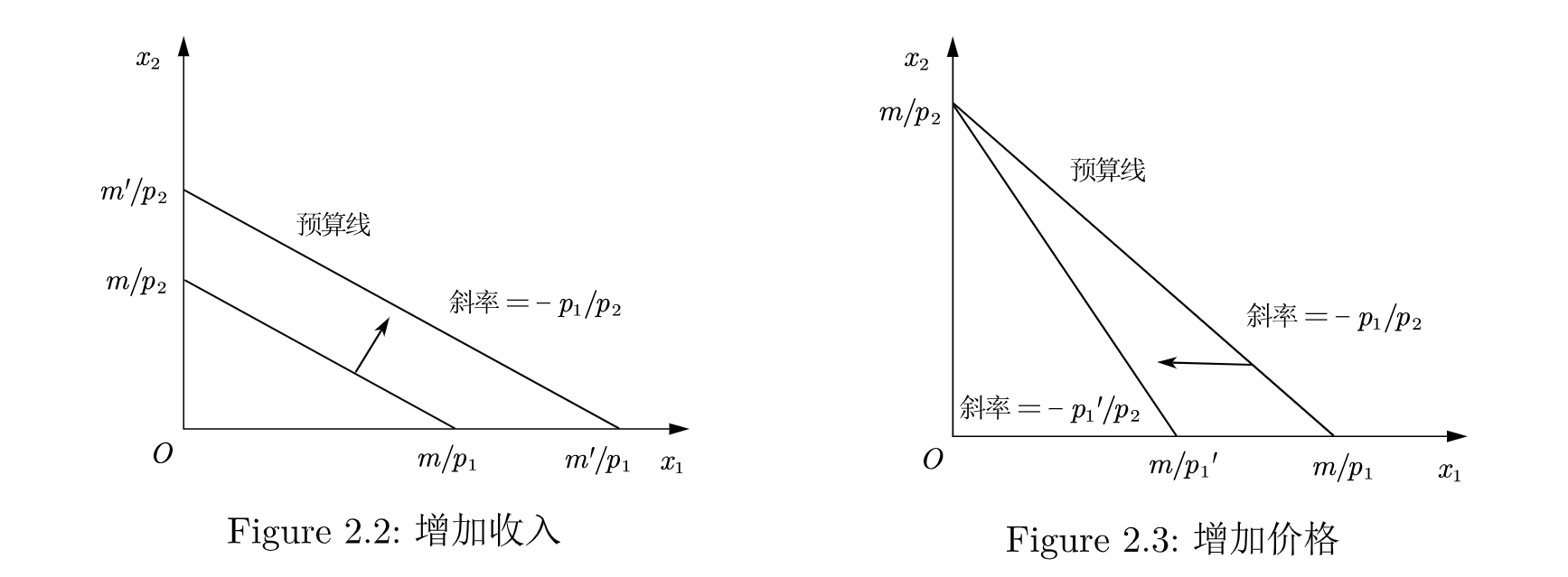
• 增加收入: 当收入增加时, 预算线向外移动, 但是斜率不变, 如 Figure 2.2.
• 增加价格1: 预算线向内移动, 斜率绝对值变大, 斜率变小, 如 Figure 2.3.

计价物

我们可以把其中一个商品或者收入看成1, 如果把一个商品价格看成1, 那么他的价格就被称为计价物(numeraire)价格.

税收、补贴和配给

• 从量税: Quantity tax, 也称消费税, 消费者购买每单位商品都需要向政府缴纳一定的税收. 对每1单位商品征收 $t$ 美元从量税, 会导致商品价格从 $p$ 变为 $p+t$.
• 从价税: Value tax, Ad valorem tax, 销售税, 对商品的价格征税, 通常用百分比表示. 对商品征收 $\tau$ 的从价税, 会导致商品价格从 $p$ 变为 $(1+\tau )p$.
• 所得税: Income tax, 对收入征税. 导致收入变少.
• 从量补贴: 根据消费者购买商品的数量给予补贴.
• 从价补贴: 根据商品的价格给予补贴.
• 总额税: 不管消费者的行为如何, 政府总要取走一笔固定金额的货币.
• 总额补贴: 不管消费者的行为如何, 政府总要给予一笔固定金额的货币.
• 配给供应: Rationing, 限制消费者购买商品的数量.

Chapter 3: 偏好

消费者偏好

• 严格偏好: $(x_1,x_2)\succ (y_1,y_2)$ 表示对于消费者来说 $(x_1,x_2)$ 严格偏好于 $(y_1,y_2)$. 偏好这个概念是建立在消费者行为基础上的.
• 无差异: $(x_1,x_2)\sim (y_1,y_2)$表示两个消费束使得消费者获得的满足程度完全一样.
• 弱偏好: 消费者在两个消费束之间有偏好或者无差异, 表示为 $(x_1,x_2)⪰(y_1,y_2)$.

关于偏好的几种假设

关于消费者偏好的三条公理:

1. 完备性公理: 假定任何两个消费束之间都是可以比较的. 也就是说, 要么有 $(x_1,x_2)⪰(y_1,y_2)$ 或 $(y_1,y_2)⪰(x_1,x_2)$ 或两者都有, 最后一种情况就说明消费者对这两个消费束是无差异的.
2. 反身性公理: 假定任何消费束至少是与本身一样好的. 也就是说, $(x_1,x_2)⪰(x_1,x_2)$.
3. 传递性公理: 假定如果 $(x_1,x_2)⪰(y_1,y_2)$ 且 $(y_1,y_2)⪰(z_1,z_2)$, 那么 $(x_1,x_2)⪰(z_1,z_2)$.

无差异曲线

• 无差异曲线: 和 $(x_1,x_2)$ 无差异的消费束.
• 弱偏好集: 弱偏好于 $(x_1,x_2)$ 的所有消费束的集合.

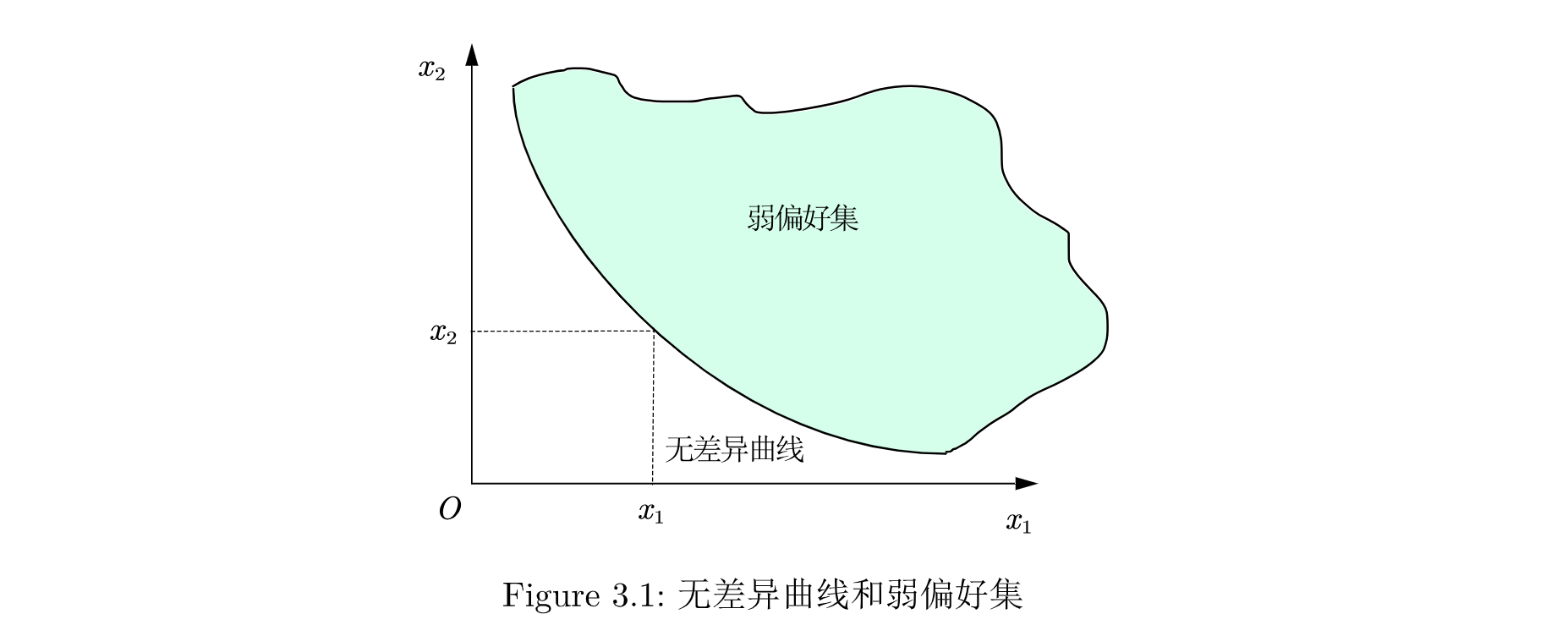
如图Figure 3.1 所示, 无差异曲线和弱偏好集.

注意, 无差异曲线之间不能相交. 我们先在每条无差异曲线上选择一个消费束, 分别记为 $X$ 和 $Y$, 然后再选择他们的交点 $Z$, 我们不妨设 $X\succ Y$, 同时注意到 $X\sim Z$, $Y\sim Z$, 这就会导出 $X\sim Y$, 这是和 $X\succ Y$矛盾的.

偏好的实例

对于某个点 $(x_1,x_2)$, 现在考虑给消费者增加一点商品1, 即 $\Delta x_1$, 现在考虑: 为了使得现在的消费束和之前的消费束无差异, 应该如何变动 $x_2$? 也就是求出 $\Delta x_2$, 使得 $(x_1+\Delta x_1,x_2+\Delta x_2)\sim (x_1,x_2)$.

完全替代品

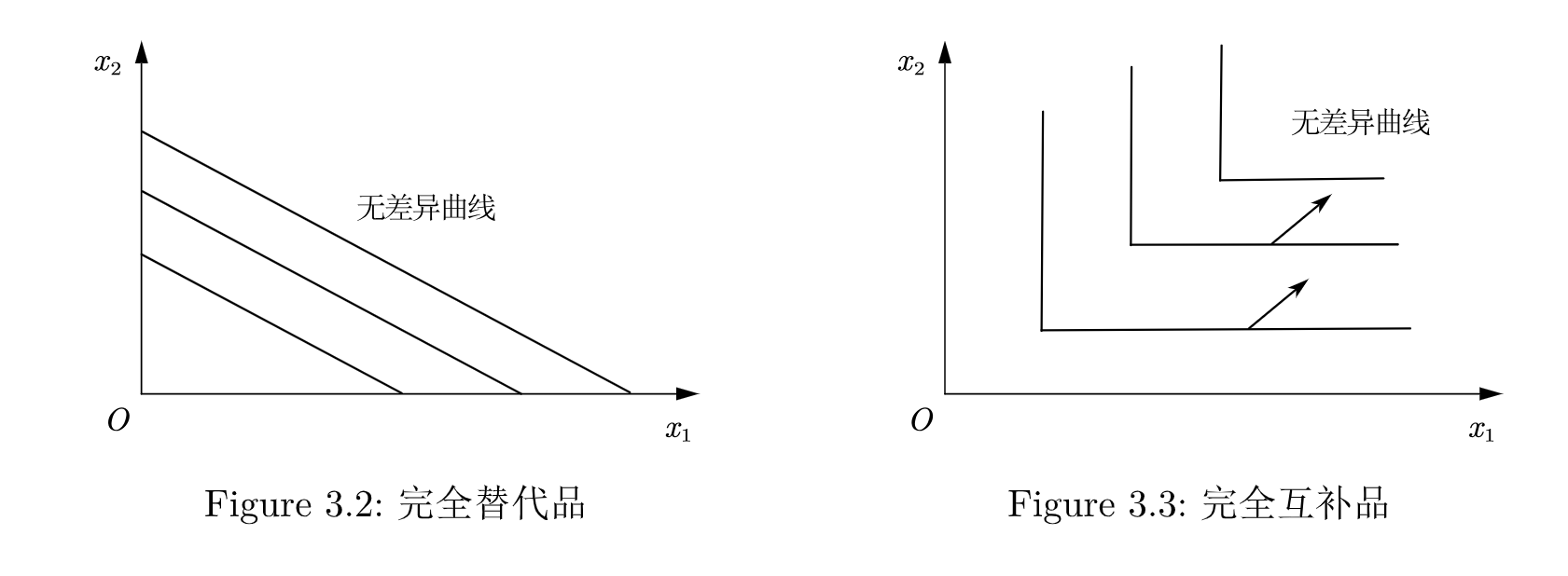
完全替代品: 消费者愿意按固定的比率用一种商品替换另一种商品. 比如, 消费者愿意用 $t$ 单位商品2来替换1单位商品1, 那么无差异曲线的斜率就为 $-t$.

在Figure 3.2中, 不同的无差异曲线分别代表不同的偏好. 但是他们的斜率都是 $-t$.

完全互补品

完全互补品: 始终以固定的比例一起消费的商品. 比如鞋子, 必须要一只左脚一只右脚, 然后你无论怎么增加右脚的数量, 都不会让消费者的效用增加, 也就是$(1,1)\sim (1,x),x>1$.

因此, 无差异曲线将是一条L型曲线, 正如Figure 3.3 所示.

厌恶品

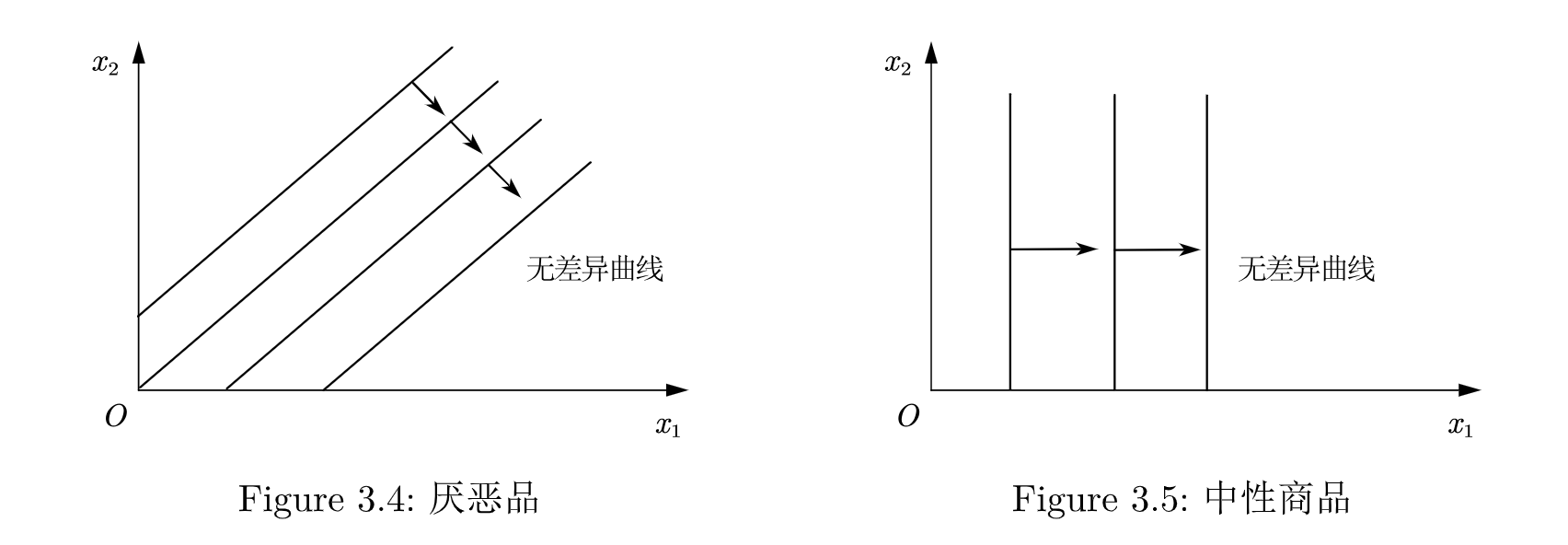
厌恶品: 消费者所不喜欢的商品. 增加厌恶品, 反而会导致消费者的效用下降. 也就是在增加 $x_1$ 的同时, 必须同时增加 $x_2$ 来补偿消费者的效用下降.

因此, 存在厌恶品的无差异曲线的斜率必然为正, 如Figure 3.4 所示.

中性商品

中性商品: 无论数量怎么增加, 消费者都毫不在乎. 比如 $x_1$ 是中性商品, 那么$(x_1,x_2)\sim (x_1^{\prime },x_2),\forall x_1^{\prime }$.

此时的无差异曲线是一条垂直线, 如Figure 3.5 所示.

魇足

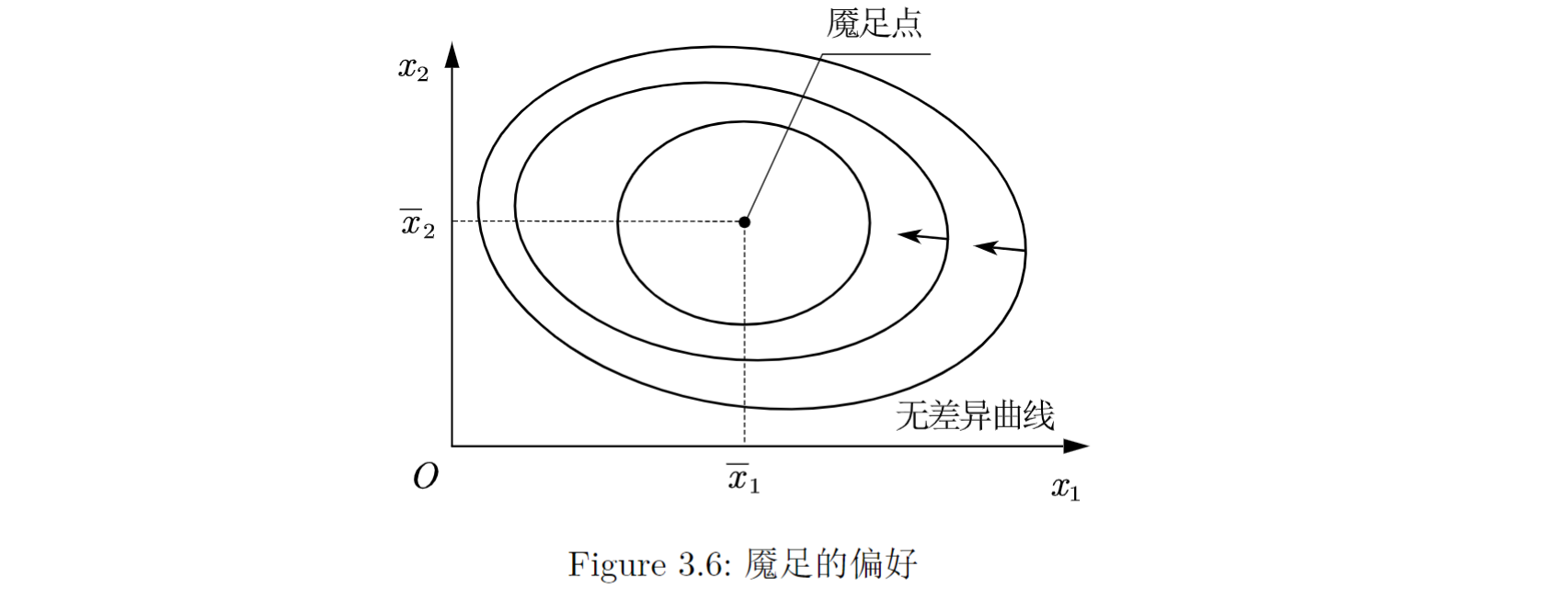
魇足: 对于消费者来说有一个最佳的消费束, 越靠近这个消费束越好. 比如, 有一个消费者最偏爱的消费束 $({\bar{x}}_1,{\bar{x}}_2)$, 离这个消费束越远, 他的情况就越糟. 那么这个点就是一个魇足点或者最佳点. 如Figure: 3.6 所示.

离散商品

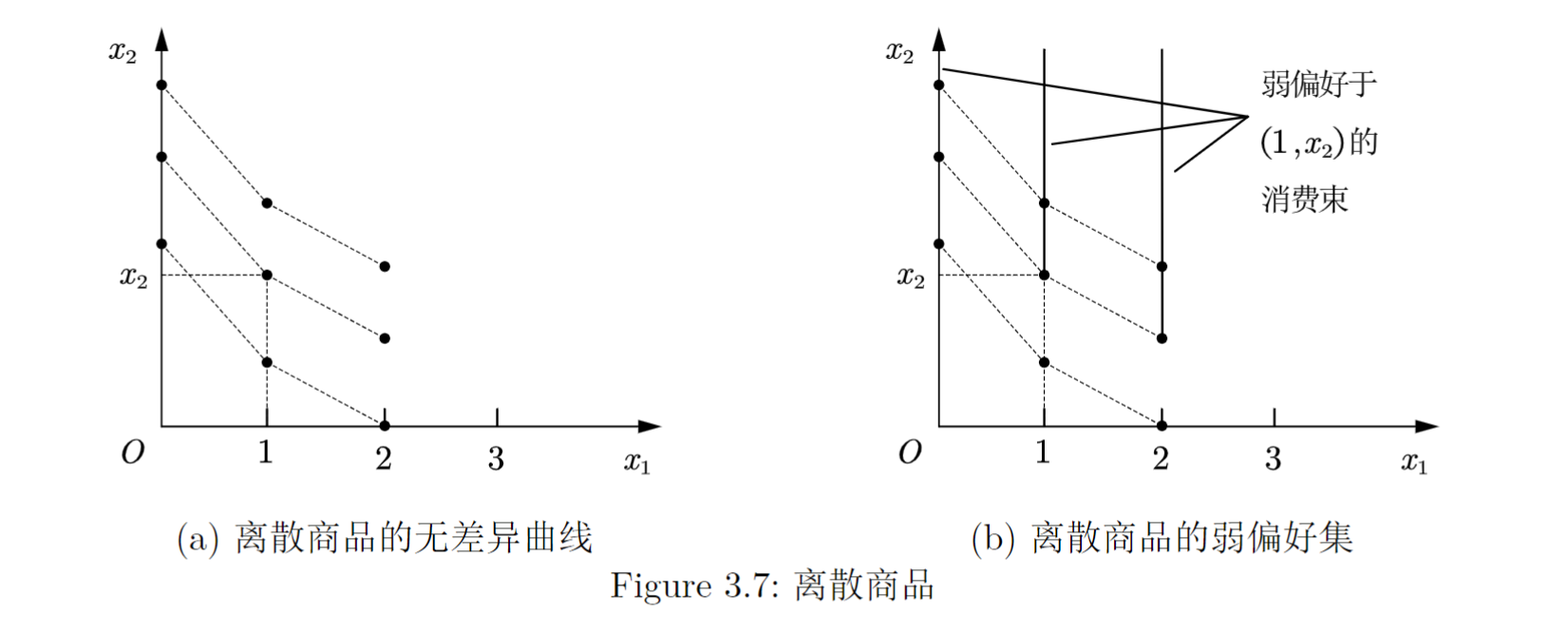
离散商品: 只能以整数量获得的商品. 我们要求出 $x_1=0$ 的时候 $x_2$ 在对应偏好下的取值, $x_1=1$ 的时候 $x_2$ 在对应偏好下的取值, $x_1=2$ 的时候 $x_2$ 在对应偏好下的取值, ..., $x_1=n$ 的时候 $x_2$ 在对应偏好下的取值. 然后把这些点连接起来.

而为了求出弱偏好集, 实际上就是在对应的整数 $x_1$ 下, 所有的 $(x_1,x_2),x_2\ge x_2^{\text{corresponding}}$. 实际上一条无差异曲线应该是一堆 $x_1$ 为整数的点的集合, 如Figure 3.7(a). 而弱偏好集则是一堆垂直的线条的集合, 如Figure 3.7(b).

选择是否强调一种商品的离散性取决于我们的应用. 比如消费者一般就选择1个或者2个单位的商品, 那么离散性很重要. 但是选择的商品数量很大, 离散型就没有那么重要了.

良态偏好

良态无差异曲线的的定义性特征:

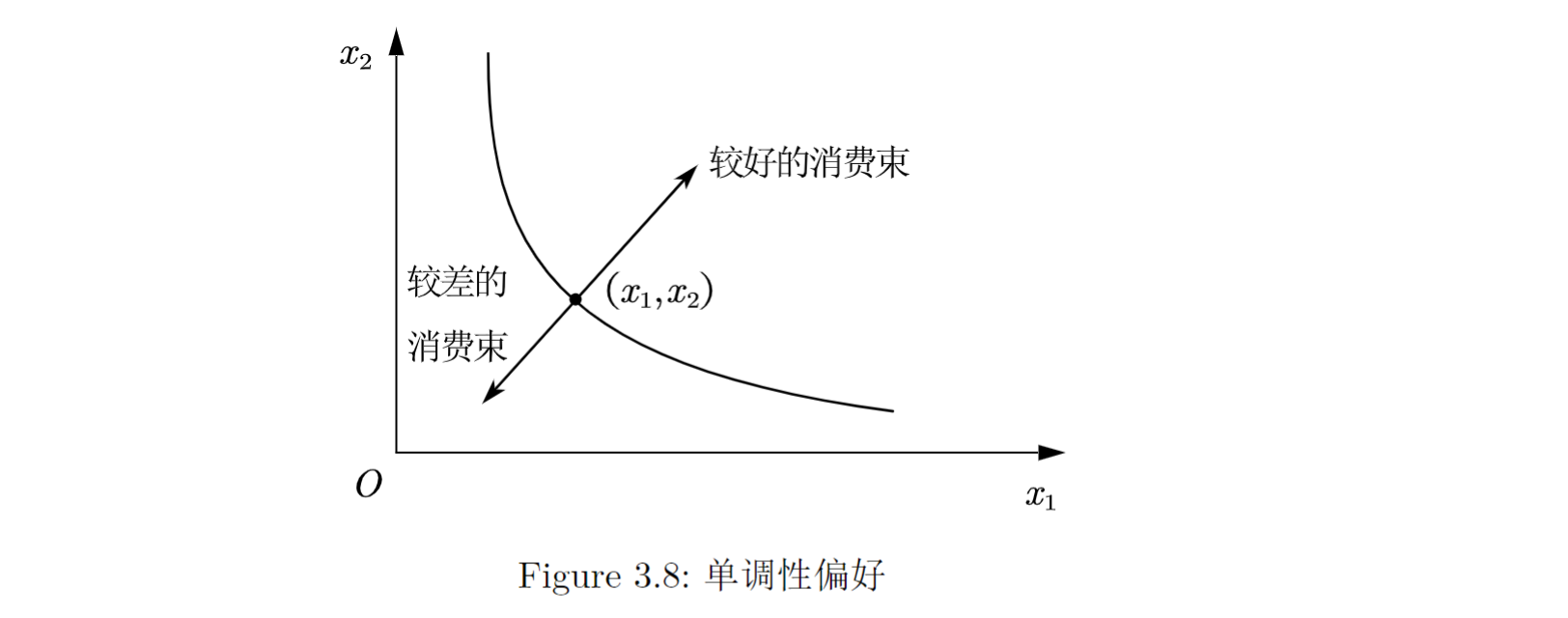
1. 就商品(goods)而不是厌恶品(bads)而言, 人们认为多多益善. 这个假设也被称为偏好的单调性. 也就是说, 假设 $(x_1,x_2)$ 是一个由正常商品组成的消费束, $(y_1,y_2)$ 是一个满足 $y_1\ge x_1,y_2\ge x_2$ 且两者不能均取等的消费束, 那么 $(y_1,y_2)\succ (x_1,x_2)$. → 无差异曲线的斜率必须是负的. 如Figure 3.8所示.

2. 平均消费束比端点消费束更受偏好. 也就是我们假定: 如果 $(x_1,x_2)\sim (y_1,y_2)$, 那么对于任何的 $t\in [0,1]$, 有: $$(t{x}_1+(1-t)y_1,t{x}_2+(1-t)y_2)⪰(x_1,x_2).$$

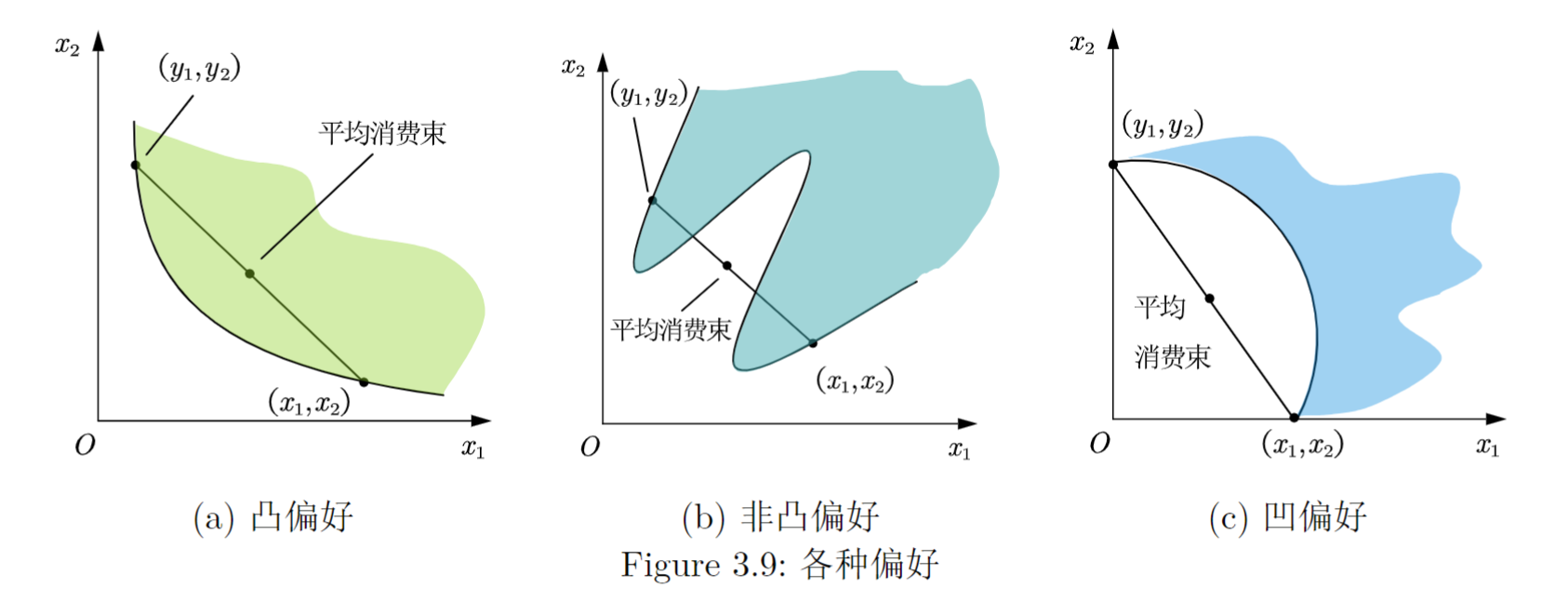
这件事在几何上的解释意味着弱偏好于 $(x_1,x_2)$ 的所有消费束的集合是一个凸集. 换句话说, $(x_1,x_2)$ 和 $(y_1,y_2)$ 的所有加权平均消费束都弱偏好于 $(x_1,x_2)$ 和 $(y_1,y_2)$.

凸集具有这样的特征, 即我们如果在集上任取两个点, 则它们的连线段完全在集内. Figure 3.9给出了各种偏好.

严格凸的, 把上面关于凸集的定义中的弱偏好于改造成严格偏好于, 凸偏好的无差异曲线可能有平坦的部分, 但是严格凸偏好的无差异曲线不存在平坦部分.

完全替代商品的偏好是凸的, 但不是严格凸的.

边际替代率

边际替代率: 无差异曲线的斜率, marginal rate of substitution, MRS. → 边际替代率一般是负数. 计算公式: $$\text{MRS}=\frac{\Delta x_2}{\Delta x_1}.$$

假设消费者具有良态偏好, 也就是说, 消费者的偏好是单调的、凸的, 现在提供一次交换商品的机会, 按照某个交换率 $E$ 来交换, 也就是消费者放弃 $\Delta x_1$ 单位的商品1, 他可以得到 $E\Delta x_1$ 单位的商品2. 那么这就意味着消费者可以沿着一条斜率为 $-E$ 的直线移动.

→ 现在问: 为了让消费者保持在$(x_1,x_2)$这个消费束上不动, 这个交换率应该是多少?

→ 那么这就意味着这条直线上的点不能出现在这条无差异曲线的上方, 否则我们就可以从上方的消费束中选择一个, 使得消费者对这个消费束有更强的偏好.

→ 这也就意味着这条直线和无差异曲线在这点相切, $-E=\text{MRS},E=-\text{MRS}$, Figure 3.10说明了这点.

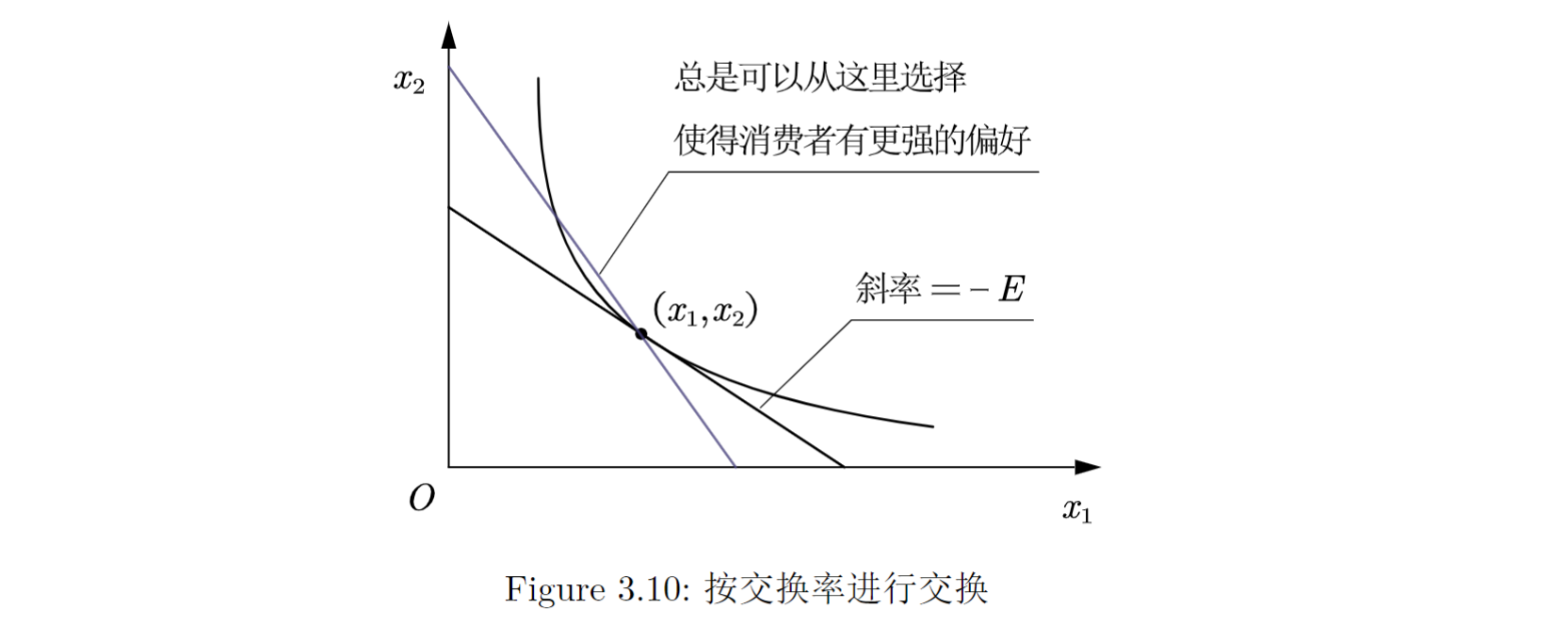
边际消费意愿: 为了多消费一点商品1而愿意放弃的美元数. 我们只需要把商品2看成美元即可.

Chapter 4: 效用

基数效用

构造效用函数

根据无差异曲线构造效用函数: 画一条如Figure 4.1的对角线, 沿着这条线测度每条无差异曲线离原点的距离, 并且以此标记每条无差异曲线. 只要偏好是单调的, 我们就可以说明这是一个效用函数.

由效用函数推出无差异曲线: 我们假设效用函数为 $u(x_1,x_2)=x_1{x}_2$. 那么无差异曲线就是使得 $k=x_1{x}_2$ 的所有 $x_1$ 和 $x_2$ 的组合. → 无差异曲线满足公式 $$x_1=\frac{k}{x_2}.$$ Figure 4.2中的三条无差异曲线就分别是 $k=1,2,3$ 的情况.

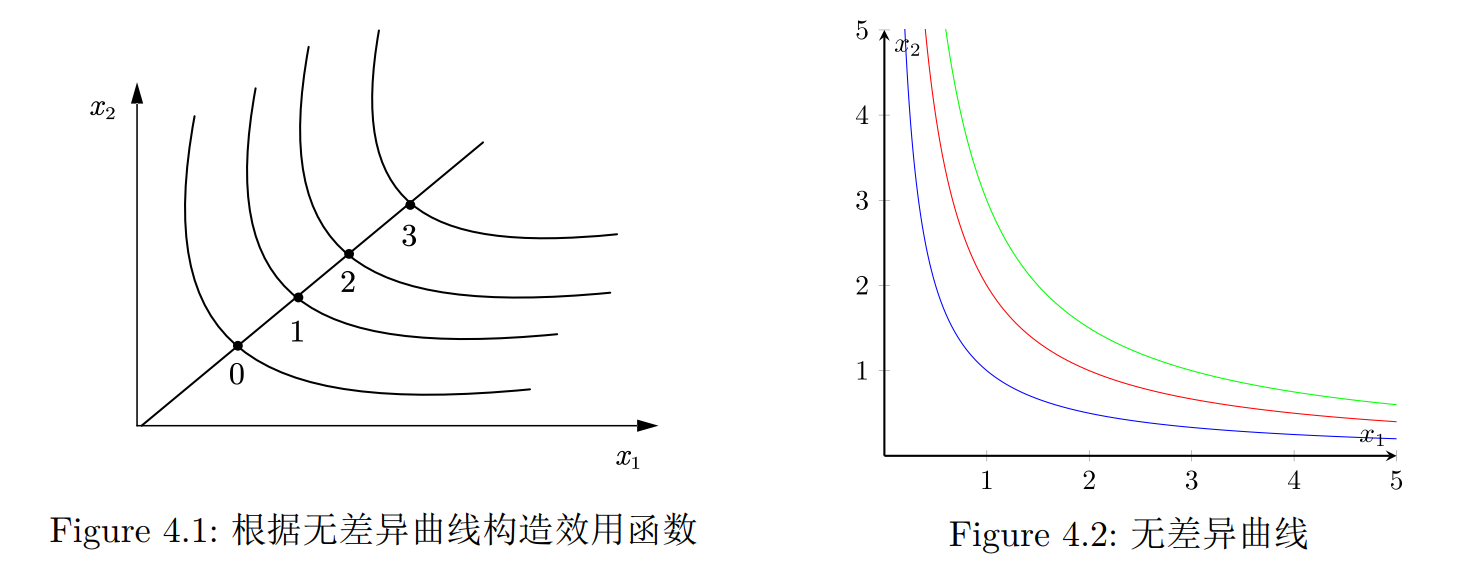
完全替代偏好

完全替代偏好: 一般地, 完全替代偏好可以使用以下形式的效用函数来描述: $$u(x_1,x_2)=a{x}_1+b{x}_2.$$

完全互补偏好

完全互补偏好: 一般地, 完全互补偏好可以使用以下形式的效用函数来描述: $$u(x_1,x_2)=\min \{a{x}_1,b{x}_2\}.$$

拟线性偏好

拟线性偏好: 效用函数对商品2来说是线性的: $$u(x_1,x_2)=v(x_1)+x_2.$$

柯布-道格拉斯偏好

边际效用

商品1的边际效用: marginal utility of good 1.

被定义为: $${\text{MU}}_1=\frac{\Delta U}{\Delta x_1}=\frac{u(x_1+\Delta x_1,x_2)-u(x_1,x_2)}{\Delta x_1}.$$ 或者是某种微积分的定义形式: $${\text{MU}}_1=\underset{\Delta x_1\to 0}{\lim }\frac{u(x_1+\Delta x_1,x_2)-u(x_1,x_2)}{\Delta x_1}=\frac{\partial u(x_1,x_2)}{\partial x_1}.$$

我们可以发现: $${\text{MU}}_1\Delta x_1+{\text{MU}}_2\Delta x_2=\Delta U=0.$$ 根据这个式子, 我们将会推导得到: $$\text{MRS}=\frac{\Delta x_2}{\Delta x_1}=-\frac{{\text{MU}}_1}{{\text{MU}}_2}.$$

通勤车票的效用

我们假设 $(x_1,x_2,...,x_n)$ 表示自己驾车时的对应的$n$个特征的值, $(y_1,y_2,...,y_n)$ 表示坐公交时的对应的$n$个特征的值. 我们设效用函数表示为: $U(x_1,x_2,...,x_n)={\beta }_1{x}_1+{\beta }_2{x}_2+...+{\beta }_n{x}_n.$

${\beta }_i$ 表示各种特征的边际效用, 两个系数之间的比率, 表示一个特征和另一个特征之间的边际替代率. e.g. $$\frac{{\beta }_1}{{\beta }_2}=\frac{{\text{MU}}_1}{{\text{MU}}_2}=-\text{MRS}.$$ 这是说, 要是能减少1单位的特征1, 消费者宁愿增加 $\text{MRS}$ 个单位的特征2.

微分表达形式

方法一: 根据 $\text{MU}$ 的计算, 我们知道: $$\mathrm{d}u=\frac{\partial u(x_1,x_2)}{\partial x_1}\mathrm{d}{x}_1+\frac{\partial u(x_1,x_2)}{\partial x_2}\mathrm{d}{x}_2=0.$$ 这样我们就会得到: $$\text{MRS}=\frac{\mathrm{d}{x}_2}{\mathrm{d}{x}_2}=-\frac{\frac{\partial u(x_1,x_2)}{\partial x_1}}{\frac{\partial u(x_1,x_2)}{\partial x_2}}.$$

方法二: 把 $x_2$ 视作 $x_1$ 的函数 $x_2(x_1)$, 那么有: $$u(x_1,x_2(x_1))\equiv k.$$ 对于这个式子两边同时对$x_1$求微分得到: $$\frac{\partial u(x_1,x_2)}{\partial x_1}+\frac{\partial u(x_1,x_2)}{\partial x_2}\frac{\partial x_2(x_1)}{\partial x_1}=0.$$ 这个方程将会得到: $$\text{MRS}=\frac{\partial x_2(x_1)}{\partial x_1}=-\frac{\frac{\partial u(x_1,x_2)}{\partial x_1}}{\frac{\partial u(x_1,x_2)}{\partial x_2}}.$$

边际替代率与效用的表示方法无关, 因为作单调变换 $f(u)$ 后得到 $\frac{\partial f}{\partial u}$ 可以消去.

单调变换不可能改变边际替代率.

柯布-道格拉斯偏好:

• 选择对数表达式: $$\text{MRS}=-\frac{c/x_1}{d/x_2}=-\frac{c{x}_2}{d{x}_1}.$$
• 选择指数表达式: $$\text{MRS}=-\frac{c{x}_1^{c-1}{x}_2^d}{d{x}_1^c{x}_2^{d-1}}=-\frac{c{x}_2}{d{x}_1}.$$

Chapter 5: 选择

消费者从他们的预算集中选择最偏好的消费束.

最优选择

预算线与无差异曲线相切的消费束是消费者的最优选择, 记为 $(x_1^{\ast },x_2^{\ast })$. 如Figure 5.1所示.

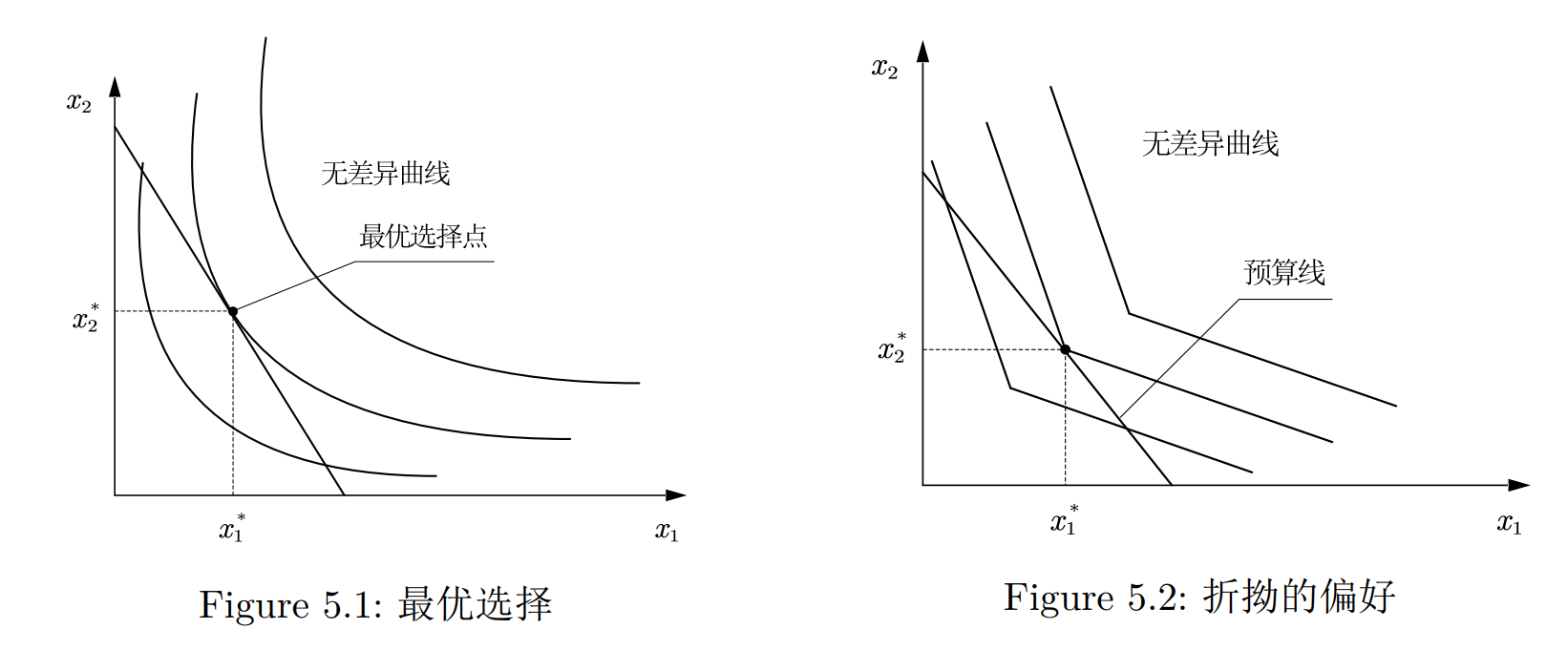
但是最优选择并不是一定意味着相切.

• 无差异曲线没有切线. 但是却有一个折点. 这种情况没有多少经济学含义, 如Figure 5.2.
• 最优选择出现在某些商品为0的情况. 虽然斜率不同, 但是无差异曲线没有穿过预算线, 比如Figure 5.3. 这代表一个边界最优, 而Figure 5.1则代表一个内部最优.
• 而且相切也不一定最优, 比如Figure 5.4.

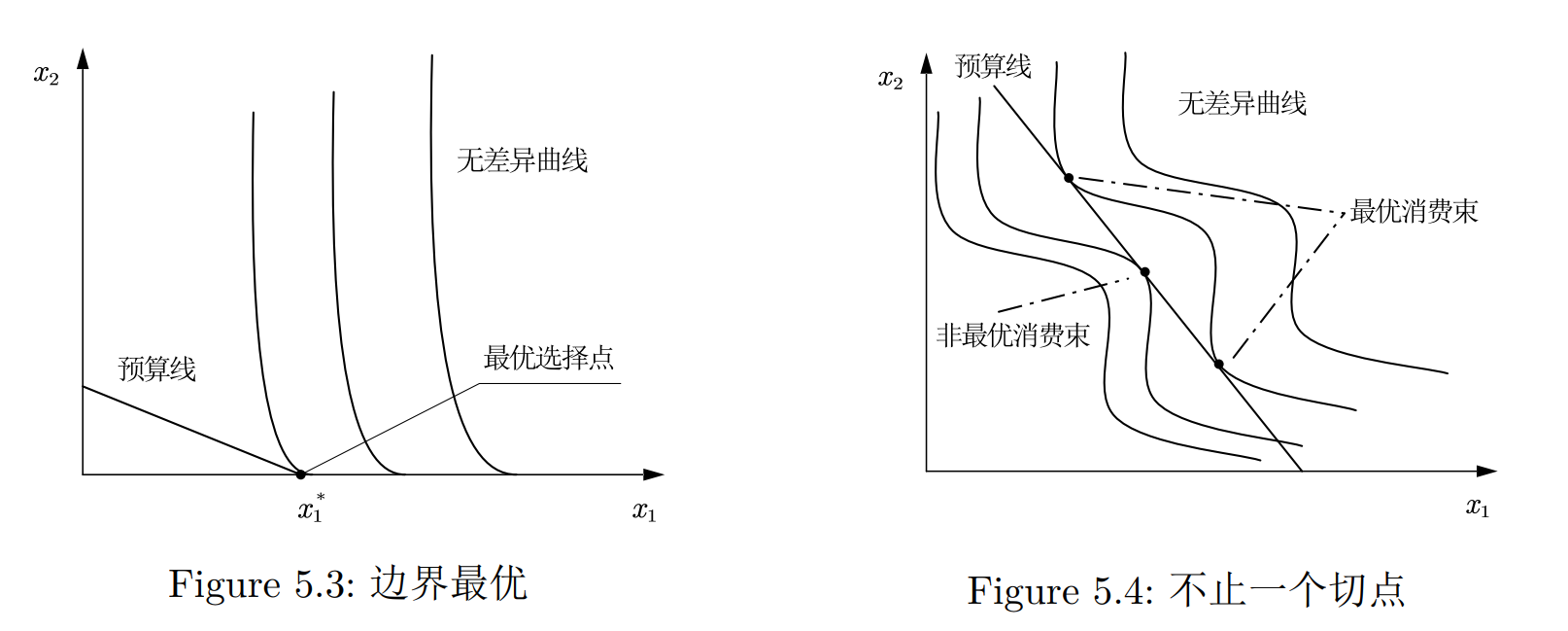
内部最优点上, 一定有: $$\text{MRS}=-\frac{p_1}{p_2}.$$我们可以发现预算约束线的斜率实际上代表了两种商品的交换比率.

消费者需求

需求束: 一定价格和收入水平下商品1和商品2的最优选择, 被称为消费者的需求束.

需求函数: 需求函数是将最优选择(也就是需求数量)与不同的价格和收入值联系起来的函数. 我们可以把需求函数记为 $x_1(p_1,p_2,m)$ 和 $x_2(p_1,p_2,m)$.

完全替代

那么消费者应该去买便宜的那一种. 所以商品1的需求函数为: $$x_1=\{\begin{array}{ll}m/p_1,& \text{ if }{p}_1<p_2,\\ \text{any value between }0\text{ and }m/p_1,& \text{ if }{p}_1=p_2,\\ 0,& \text{ if }{p}_1>p_2.\end{array}$$

完全互补

最优选择应该总是出现在对角线上. e.g. 应该成对地买鞋. $$x_1=x_2=\frac{m}{p_1+p_2}.$$

中性商品和厌恶品

消费者应该会把所有的钱购买他喜爱的商品, 所以这两类商品的需求都为0.

离散商品

分别比较 $(0,m)$, $(1,m-p_1)$, $(2,m-2p_1)$, ...来判断哪个消费束的效用最高. 我们这里假设商品2是美元, 而商品1是只能以整数单位获得的商品.